- Apakah graf pada gambar di bawah mempunyai sirkuit Euler? Jelaskan!
A
B
Jawab:
Untuk mengetahui
apakah graf A di atas memiliki sirkuit Euler, kita dapat menggunakan
suatu teorema yang menyatakan “Jika pseudograf G terhubung dan derajat
setiap titiknya mempunyai derajat genap, maka G mempunyai sebuah sirkuit
Euler” Untuk itu kita periksa bahwa A terhubung dan derajat
setiap titiknya genap. Pertama kita beri label setiap titik dan sisi pada
graf A sebagai berikut:
A
Graf A terhubung
karena terdapat sebuah lintasan dari titik x dan y jika diketahui sembarang
titik x dan y. Dan jika kita periksa sebagai berikut:
a ke b
lintasannya (a, e1, b) ; a ke c lintasannya (a, e1, b, e2, c) ; a ke
d lintasannya (a, e12,d) ; a ke e lintasannya (a, e11, e) ; a ke
f lintasannya (a, e11, e, e10, f) ; b ke c lintasannya (b, e2, c) ;
b ke d lintasannya (b, e4, d) ; b ke e lintasannya (b, e4, d, e8,e) ; b ke f
lintasannya (b, e6, f) ; c ke lintasannya (c, e7, f, e9, d) ; c ke e
lintasannya (c, e5, e) ; c ke f lintasannya (c, e7, f) ; d ke e
lintasannya (d, e8, e) ; d ke f lintasannya (d, e9, f) ; e ke f lintasannya (e,
e10, f) ; sehingga dengan demikian A terhubung.
d(a) = d(b)
= d(c) = d(d) = d(e) = d(f) = 4 ini artinya setiap setiap
titik pada graf A berderajat genap.
Karena derajat
setiap titik adalah genap, menurut teorema tersebut di atas maka A mempunyai
sebuah sirkuit Euler.
Jadi graf A di
atas mempunyai Sirkuit Euler-nya, dan sirkuit Euler-nya yaitu:
- Jika diberikan sembarang simple graf, sebagai berikut:G = (V, E); V = {1, 2, 3, 4, 5, 6}; E = {13, 14, 15, 16, 23, 24, 26, 35, 36, 46, 56} Apakah graf G tersebut merupakan graf planar?Jawab

- Dept. IF mempunyai 6 kelompok kerja yang setiap bulannya masing-masing selalu mengadakan rapat satu kali. Keenam kelompok kerja dengan masing-masing anggotanya adalah: K1 = {Amir, Budi, Yanti}, K2 = {Budi, Hasan, Tommy}, K3 = {Amir, Tommy, Yanti}, K4 = {Hasan, Tommy, Yanti}, K5 = {Amir, Budi}, K6 = {Budi, Tommy,Yanti}.
Berapa banyak waktu rapat berbeda yang harus direncanakan sehingga
tidak ada anggota kelompok kerja yang dijadwalkan rapat pada waktu yang sama.
Gambarkan graf yang merepresentasikan persoalan ini lalu (sisi menyatakan apa,
simpul menyatakan apa) tentukan jumlah waktu rapat ini.
Jawab :
Simpul :
menyatakan kelompok
Sisi :
menyatakan adanya anggota kelompok yang sama
Jika
ada sisi yang menghubungkan 2 kelompok berarti kelompok tersebut tidak boleh
rapat pada waktu yang sama.
Dapat
dilihat gambar graf yang terbentuk. Untuk mencari jumlah minimum waktu rapat
yang harus disediakan kita dapat menggunakan cara yang sama seperti mencari
bilangan kromatis dari graf tersebut. Setiap warna yang berbeda mewakili satu
waktu rapat yang dibutuhkan.
Bilangan
kromatis graf tersebut adalah 5. maka waktu rapat yang harus disediakan adalah
5.
1
waktu untuk K1
1
waktu untuk K2
1
waktu untuk K3
1
waktu untuk K4 dan K5
1 waktu untuk K6
- Himpunan garis yang menghubungkan tiap node / vertex disebut ...
Jawaban :
Edge
Penjelasan :
Terlihat bahwa spanning tree tersebut mempunyai total bobot 2 + 3 + 4 +
4 + 4 + 4 + 3 = 24
- Berapa jumlah maksimum dan jumlah minimum simpul pada graf sederhana yang mempunyai 16 buah sisi dan tiap simpul berderajat sama dan tiap simpul berderajat ≥ 4 ?
Jawab:
Tiap simpul berderajat sama -> graf teratur.
* Jumlah sisi pada graf teratur berderajat r adalah e = nr/2. Jadi, n = 2e/r = (2)(16)/r = 32/r.
* Untuk r = 4, jumlah simpul yang dapat dibuat adalah maksimum, yaitu n = 32/4 = 8.
* Untuk r yang lain (r > 4 dan r merupakan pembagi bilangan bulat dari 32):
r = 8 -> n = 32/8 = 4 -> tidak mungkin membuat graf sederhana.
r = 16 -> n = 32/16 = 2 -> tidak mungkin membuat graf sederhana.
* Jadi, jumlah simpul yang dapat dibuat adalah 8 buah (maksimum dan minimum).
* Jumlah sisi pada graf teratur berderajat r adalah e = nr/2. Jadi, n = 2e/r = (2)(16)/r = 32/r.
* Untuk r = 4, jumlah simpul yang dapat dibuat adalah maksimum, yaitu n = 32/4 = 8.
* Untuk r yang lain (r > 4 dan r merupakan pembagi bilangan bulat dari 32):
r = 8 -> n = 32/8 = 4 -> tidak mungkin membuat graf sederhana.
r = 16 -> n = 32/16 = 2 -> tidak mungkin membuat graf sederhana.
* Jadi, jumlah simpul yang dapat dibuat adalah 8 buah (maksimum dan minimum).
- Pada gambar dibawah, tentukan Derajat dari graf G, Jika order dari G = n, size dari G = e, dan banyak komponen = k, berapa Rank dari graf G? Berapa jarak maksimum atau diameter dalam graf G?
- Derajat dari Graf G :
Dik: Banyak ruas = 10
Derajat Graf(G) = 2 * banyak ruas
= 2 * 10
= 20
- Cara mencari Rank dari graf tersebut adalah:
Dik
: n = 7
k = 1
Rank (G) = n – k
= 7 – 1
= 6
- Jarak maksimum pada graf tersebut adalah 3 yaitu dari A ke G, B ke G, C ke G ataupun sebaliknya.
- Jika diberikan sembarang simple graf, sebagai berikut:G = (V, E); V = {1, 2, 3, 4, 5, 6}; E = {13, 14, 15, 16, 23, 24, 26, 35, 36, 46, 56} Apakah graf G tersebut merupakan graf planar?
Jawab :
G = z(V, E); V = {1, 2, 3, 4, 5,
6}; E = {13, 14, 15,
16, 23, 24, 26, 35, 36, 46, 56}Dari
himpunan graf dan ga mbar d iperoleh:V = 6; E = 11; dan F = 7 sehingga V
– E + F = 2 (terbukti)
- Sebutkan 3 bentuk graf yang bukan merupakan graf planar (setiap graf hanya bolehdisebutkan dengan istilah yang Anda kenal, bukan dalam bentuk representasi graf: himpunangraf, matriks adjacent, ilustrasi graf).
Jawab :
K5,K3,3, dan graf tidak terkoneksi.
- Gambarlah sebuah graf sederhana yang dapat di bentuk dari 4 titik {a,b,c,d} dan 2 garis.
Jawab
:
Sebuah
garis dalam graf sederhana selalu berhubungan dengan 2 titik.Oleh karena ada 4
titik,maka ada C(4,2) = 6 garis yang mungkin di buat. Yaitu garis – garis
dengan titik ujung {a,b},{a,c},{a,d},{b,c},{b,d},{c,d}.
Dari
keenam garis yang mungkin tersebut,selanjutnya dipilih 2 garis diantaranya.jadi
ada C(6.2) = 15 buah graf yang mungkin di bentuk dari 4 buah titik dan 2 buah
garis.
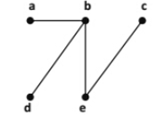
- Carilah Pohon rentang dari setiap graf –graf pada gambar di bawah inidengan menghapus jalur – jalur dalam sikel
Jawab :
Kita hapus jalur ab untuk merusak sikel a,b,d,a dan jalur bc untuk
merusak sikel b,c,e,b
Kita hapus jalur db untuk merusak sikel a,b,d,a dan jalur be untuk
merusak sikel b,c,e,b
Kita hapus jalur ad untuk merusak sikel a,b,d,a dan jalur ce untuk
merusak sikel b,c,e,b
Kita hapus
jalur ab untuk merusak sikel a,b,d,a dan jalur ec untuk merusak sikel b,c,e,b

Kita hapus jalur bd untuk merusak sikel a,b,d,a dan jalur ec untuk
merusak sikel b,c,e,b
Kita hapus
jalur ad untuk merusak sikel a,b,d,a dan jalur bc untuk merusak sikel b,c,e,b
Kita hapus
jalur bd untuk merusak sikel a,b,d,a dan jalur bc untuk merusak sikel b,c,e,b
Kita hapus
jalur bd untuk merusak sikel a,b,d,a dan jalur bc untuk merusak sikel b,c,e,b

















Tidak ada komentar:
Posting Komentar